La volatilità nel mercato azionario
La volatilità è la misura statistica della dispersione dei rendimenti per un determinato indice di titolo o di mercato. La volatilità può essere misurata utilizzando la deviazione standard o la varianza tra i rendimenti dello stesso indice di titolo o mercato. In genere, maggiore è la volatilità, più rischiosa è la sicurezza.

La volatilità nel mercato azionario
La volatilità è una variabile nelle formule di determinazione dei prezzi delle opzioni che mostrano in quale misura il rendimento dell’attività sottostante oscillerà tra la data e l’ora della scadenza dell’opzione. La volatilità, espressa come un coefficiente di percentuale all’interno delle formule di determinazione dei prezzi delle opzioni, deriva dalle attività di trading giornaliere. Il modo in cui viene misurata la volatilità influirà sul valore del coefficiente utilizzato.
La volatilità si riferisce alla quantità di incertezza o rischio correlata alla dimensione dei cambiamenti nel valore di un titolo. Una maggiore volatilità significa che il valore di un titolo può potenzialmente essere distribuito su un più ampio intervallo di valori. Ciò significa che il prezzo del titolo (leggi anche: Perché Oscilla Il Prezzo di Un Titolo?) può cambiare drasticamente in un breve periodo di tempo in entrambe le direzioni. Una minore volatilità significa che il valore di un titolo non cambia in modo drammatico e tende ad essere più costante.
La misura della volatilità relativa ad un determinato titolo sul mercato è la sua beta. Una beta approssima la volatilità complessiva dei rendimenti di un titolo rispetto ai rendimenti di un benchmark rilevante (in genere viene utilizzato l’indice S & P 500). Ad esempio, un’azione con un valore beta di 1.1 ha storicamente spostato il 110% per ogni spostamento del 100% nel benchmark, in base al livello di prezzo. Al contrario, un’azione con una beta di 0,9 si è storicamente spostata del 90% per ogni spostamento del 100% nell’indice sottostante.
La volatilità nel mercato azionario: come si calcola
La volatilità viene spesso calcolata utilizzando la varianza e la deviazione standard. La deviazione standard è la radice quadrata della varianza.
Per una più semplice spiegazione, supponiamo di avere prezzi di chiusura mensili delle azioni da 1 a 10 euro. Ad esempio, il primo mese è 1 euro, il secondo mese è 2 euro e così via.
Per calcolare la varianza, segui i cinque passaggi che seguono:
- Trova la media dell’insieme di informazioni.
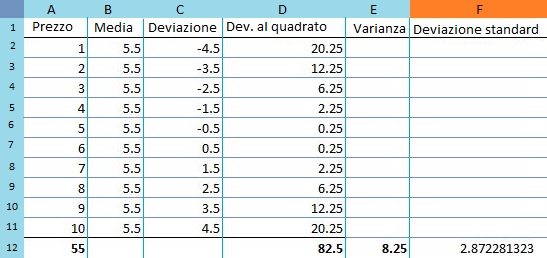
Per farlo, bisogna aggiungere ciascun valore e quindi dividerlo per il numero di valori. Se aggiungiamo 1 euro più 2 euro, più 3 euro, fino ad arrivare a 10 euro, otteniamo 55 euro. Questo risultato deve essere diviso per 10, perché abbiamo 10 numeri nel nostro insieme di dati. Questo darà la media del prezzo, che in questo caso è di 5.50 euro. -
Calcola la differenza tra ciascun valore di dati e la media.
Questo procedimento viene spesso chiamato deviazione. Ad esempio:10 euro- 5,50 euro= 4,50 euro, quindi 9 euro- 5,50 euro= 3,50 euro.
Questo procedimento è da svolgere fino al nostro primo valore di 1 eurp. I numeri negativi sono ammessi. Dal momento che abbiamo bisogno di ciascun valore, questi calcoli vengono spesso svolti in un foglio di calcolo.
- Elimina tutte le deviazioni.
Questo eliminerà i valori negativi. - Addiziona tutte le deviazioni messe al quadrato.
Seguendo il nostro esempio, otterremo 82.5. - Dividi la somma delle deviazioni al quadrato (82.5) per il numero dei valori dei dati.
In questo caso, il risultato della varianza è di 8,25 dollari. La radice quadrata viene presa per ottenere la deviazione standard. Vedremo dunque che questo calcolo equivarrà a 2,87 dollari. Questa è una misura del rischio e mostra come i valori siano distribuiti intorno al prezzo medio. Fornisce ai trader un’idea di quanto il prezzo possa discostarsi dalla media.
Se i prezzi sono distribuiti casualmente (e spesso non lo sono), allora circa il 68% di tutti i valori dei dati rientrerà in una deviazione standard. Il 95% dei valori dei dati rientrerà in due deviazioni standard (2 x 2,87 nel nostro esempio) e il 99,7% di tutti i valori rientrerà in tre deviazioni standard (3 x 2,87). In questo caso, i valori da 1 euro a 10 euro non si distribuiscono casualmente su una curva a campana, piuttosto c’è una significativa tendenza verso l’alto. Pertanto, tutti i valori non rientrano in tre deviazioni standard. Nonostante questa limitazione, la deviazione standard è ancora frequentemente utilizzata dai trader, poiché l’insieme dei dati del prezzo spesso contengono movimenti su e giù, che assomigliano più a una distribuzione casuale.
